Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- 싸피 합격
- 싸피
- 호스팅이란?
- 플로이드 워셜
- 프록시서버
- 플로이드 와샬
- 싸피 면접 후기
- 동기화
- Proxy Server
- Dijkstra Algorithm
- Synchronization
- 세마포어
- 서버 호스팅
- 세마포어와 뮤텍스
- 세마포어와 뮤텍스의 차이
- 다익스트라 알고리즘
- 프록시
- 웹 호스팅
- 삼성 청년 SW 아카데미
- 세마포어란?
- 클라우드 서버
- 뮤텍스란?
- 다익스트라
- Proxy
- SSAFY
- 호스팅
- floyd-warshall
- 최단 경로
- 뮤텍스
Archives
- Today
- Total
어제의 나보다 성장한 오늘의 나
위상정렬 (Topological Sort) 본문
개념
- 어떤 일을 하는 순서를 찾는 알고리즘이다. → 즉, 방향 그래프(단 방향 그래프)에 존재하는 각 정점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것.
- '순서가 정해져 있는 작업'을 차례로 수행해야 할 때 그 순서를 결정해 주기 위해 사용하는 알고리즘
특징
- 단 방향 그래프여야 한다.
- 위상 정렬의 과정에서 선택되는 정점의 순서를 위상 순서(Topological Order)라 한다.
- 위상 정렬의 과정에서 그래프에 남아 있는 정점 중에 진입 차수가 0인 정점이 없다면, 위상 정렬 알고리즘은 중단되고 이러한 그래프로 표현된 문제는 실행이 불가능한 문제가 된다. ( 사이클이 발생하는 경우 위상정렬 불가능 )
- 하나의 방향 그래프에는 여러 위상 정렬이 가능하다.
- 다음과 같이 4학년 루트로 갔다가 졸업하기, 학과 사이트 가입하고 졸업하기 방법처럼 다양한 순서가 나올 수 있다.
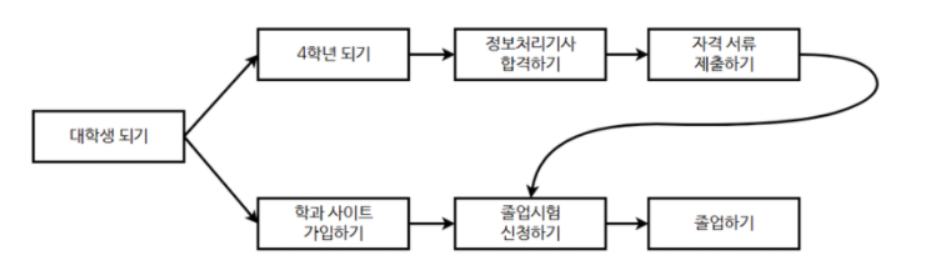
예제

- 진입 차수가 0인 정점을 큐에 삽입한다.
- 큐에서 원소를 꺼내 연결된 모든 간선을 제거한다.
- 간선 제거 이후에 진입차수가 0이 된 정점을 큐에 삽입한다.
- 큐가 빌 때까지 2번~3번 과정을 반복한다. 모든 원소에 방문하기 전에 큐가 빈다면 사이클이 존재하는 것이고, 모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상 정렬이다.
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.StringTokenizer;
public class 위상정렬 {
private static int V, E;
private static int[] inDegree, result;
private static List<List<Integer>> graph;
public static void topologySort() {
Queue<Integer> qu = new LinkedList<Integer>();
for(int i = 1; i<=V; i++) {
if (inDegree[i] == 0) qu.offer(i);
}
for(int i = 1; i<=V; i++) {
// 정점을 다 방문 하기 전에 큐가 빈다면 사이클 발생
if(qu.isEmpty()) return;
int x = qu.poll();
result[i] = x;
for (int v : graph.get(x)) {
inDegree[v]--;
if(inDegree[v] == 0) {
qu.offer(v);
}
}
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken()); // 정점 갯수
E = Integer.parseInt(st.nextToken()); // 간선 갯수
inDegree = new int[V + 1];
result = new int[V + 1];
graph = new ArrayList<>();
for (int i = 0; i < V+1; i++) {
graph.add(new ArrayList<Integer>());
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int first = Integer.parseInt(st.nextToken()); // 정점 갯수
int last = Integer.parseInt(st.nextToken()); // 간선 갯수
graph.get(first).add(last);
inDegree[last]++;
}
topologySort();
for (int i = 1; i <= V; i++) {
System.out.println(result[i] + " ");
}
}
}시간복잡도
O(V+E)이다. 즉, 정점의 개수 + 간선의 개수만큼 소요되므로 매우 빠른 알고리즘 중 하나
출처
'공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 에라토스테네스의 체 ( 소수 구하기 ) (0) | 2021.06.04 |
|---|---|
| 플로이드 와샬(Floyd-Warshall) (0) | 2021.04.08 |
| 유클리드 호제법 - 최소공약수, 최대공배수 (0) | 2021.04.04 |
| 다익스트라 알고리즘(Dijkstra Algorithm) (1) | 2021.04.03 |
Comments



